論文のリンク
論文ほんへんリンク(Appendixあり)
Introduction
PU Learningは文書分類、外れ値検束、医療診断、時系列分類などで使われてきた。
この論文ではPNU+Importance Weightingをしている。出現頻度が低いUnlabeledのデータの重みを大きくしてる感じ。
この論文での貢献
- PU biased N Learningの定式化を行い、性能を実験で確認して理論的にも下界評価した。
- Negativeのデータはbiasedとはいえ、使った方が純粋なPUよりも性能が上がった。
- この手法はPUbNだけではなく、純粋なPUにも還元できるし、性能もトップクラスだった。
Relation with Semi-supervised Learning
PNUの全てがそろっているときに適用できる自己教師学習と似ている。しかし、この研究ではrisk estimatorを減らしているし、そもそもNのデータはbiasedで少量しかないことが前提。その上、Unlabeledは学習の上で重みを付けて、risk estimatorの最小化という扱いだ。
だが、自己教師学習はUnlabeledの大量のデータを使って学習過程のモデルの安定性や一般化能力を高める正則化?をするという意味で、目指すものが違う。
Relation with Data Shift
訓練しているデータの分布が違う分野に移す転移学習?と似ている。というか、bNからUへ転移学習しているともいえる。共変量シフトもそうだよね。
また、ソースが複数の分布から生じるとして、trainとtestでその構成比が異なる場合でも訓練=Source Component Shiftとも関係があると言える。この研究もこれに属すると言えるが、そもそもこの分野には一般的な手法がないのでどうしようもない。
Problem Setting
基本的な文字の定義は xはデータ、 y∈{−1,+1}はground truthの属性である。損失関数 lは正の値なら基本的に0で負の値なら大きくなる。
Positive Negative Learning
学習器 g(x)で上手く yを予測したい。以下の分類リスクを最小化したい。
R(g)=Ex,y[l(yg(x))] 01損失が一番理想的であるが傾きがなので、代理損失を一般的に使うことになる。代わりは以下のようなものが多い。
sigmoidlossl(x)=1+ex1logisticlossl(x)=log(1+e−x) 訓練データはすべてラベルが明確についており、最小化するのは偽陽性(negativeなのにpositiveにされる)と偽陰性(positiveなのにnegativeにされる)の、クラス事前確率(与えられている) π=p(y=+1)を乗じたものである。(リスクは01損失を使った時は偽陰性、偽陽性の確率とみなせるので書き換えは自然)
R(g)=πE(x,y)∈XP[l(g(x))]+(1−π)E(x,y)∈XN[l(−g(x))] Positive Unlabeled Learning
Negativeデータないので、Unlabeledでやるしかない。ad hocなやり方が多いが、duPlessisのcost-sensitiveの方法[nPU]だと以下の式を使って最適化をする。
Ex∼p(x)[l(−g(x))]=πEp(x∈p(x,+1))[l(−g(x))]+(1−π)Ep(x∈p(x,−1))[l(−g(x))] これを使って変形すると、以下のリスク関数を最小化する。
R(g)=π(Ex∈p(x,+1)[l(g(x))−l(−g(x))])+Ex∈p(x)[l(−g(x))] ここで、対称ロスなどで改善できたりするという話がある。
このなかで、DNNなどの表現力が高すぎるモデルだと過学習して R(g)がマイナスに行くので、Kiryo2017[nnPU]で提案されるのは、以下の改良されたリスク関数を最小化する。
R(g)=πEx∼p(x,1)[l(g(x))]+max(0,Ex∼p(x)[l(−g(x))],−πEx∼p(x,1)[l(−g(x))]) 実装上、 maxの項の中である閾値より小さくなったときに、過学習を防ぐために、勾配上昇法といって、勾配降下法とは別に逆に勾配の向きで大きくなるように頑張って登ったりもする。
Positive Negative Unlabeled Learning
📄 2017-ICML-[PNU]Semi-Supervised Classification Based on Classification from Positive and Unlabeled Data で提案されたPNU Learningという手法がある。PNU Learningのリスクは、PNとPU or NUの適宜な割合 γでの混合比で混ぜたものである
2017-ICML-[PNU]Semi-Supervised Classification Based on Classification from Positive and Unlabeled Data で提案されたPNU Learningという手法がある。PNU Learningのリスクは、PNとPU or NUの適宜な割合 γでの混合比で混ぜたものである
原文に誤植あり。この式のR(g)の1項目にπがない。
この論文も結局この式をうまく計算して最小化させる形になる。
Positive Unlabeled biased Negative Learning
PUの仮定通りと似ているが、ラベルがつくかどうかの s∈{−1,+1}として、以下のことが前提として成り立つ。
∀x,p(s=+1∣x,y=+1)=1∀x,p(y=−1∣x,s=−1)=1 この sは一部のNegativeサンプルに対して、ラベルが付いていることを指し示す潜在変数。
- 一番上は、PositiveのGround-truthを持つサンプルについて、サンプルx次第でPとしてラベルがつくかどうかが決まるという意味。
- 二番目は、ラベルがつかないサンプルについて、サンプルx次第でNegativeであるかどうかがわかるという意味。
例として、文書分類を考える。Negativeに相当するのはN個のカテゴリがあるとき、ラベル付けされるのはそのうちのMカテゴリで、M<Nである。なので、ラベル付けされたNegativeは、Negativeの全体の分布からずれている、Biased Negativeということ。
ρ=p(y=−1,s=+1)とground truthがNなのに、ラベル付けされる確率(そのようにラベル付けされたNegativeはbiased Negative)を置く。
π,ρはいずれもうまいこと推定してから事前確率として扱うのが多い。よってbiased Negativeは事前条件 ρ=p(y=−1,s=+1)の下で、以下のように、集めている。
この考え自体、ラベル付けに誤りがあると考えるNoisy Labelと似ている?同じラベルついていると扱われているのにNegativeである、とも考えられる。
Method
この式の意味は、
- 確率 π=p(y=+1)を重みとして、Ground-truthがPositiveであるデータ全てに対しての損失を加える。
- 確率 ρ=p(y=−1,s=+1)を重みとして、 s=+1としてラベルが付いてるが 、Ground-TruthがNegativeのデータ全てに対しての損失を加える。
- 確率 1−π−ρ=p(s=−1,y=−1)を重みとして、ラベル付けされてないすべてのGround-TruthがNegativeのデータ全てに対しての損失を加える。
このうち、以下のように前の2項は計算で得ることができる。これはデータとしては、Positiveとbiased Nとして使われる。
EP[l(g(x))]≈nP1∑i=1nPl(g(xiP))Ex∣y=−1,s=+1[l(−g(x))]≈nbN1∑i=1nbNl(−g(xibN)) この式で予測しているからには、Positiveの選択には選択バイアスがないことを前提にしている。
となると、 Ex∣y=−1,s=−1[l(−g(x))]をどのように推計するんか?という問題になる。
σ(x)=p(s=+1∣x)∀η∈[0,1]h:Rd→[0,1]∩h(x)>η⇒σ(x)>0 あるデータを受け取り、 [0,1]へ写す hがあるとして(これは識別器ではない)、それがどんな閾値 ηでも、それを超えるのならば、 σ(x)=p(s=+1∣x)>0が成り立つという前提条件を考える。この時、以下のような証明1で式変形できる。( σ(x)はpropensity scoreともいえる)
どんなηでも、h(x)>ηが満たされるなら、σ(x)=0ではない=ラベルがつきうるので損失関数の計算に含める必要があるという前提をとる、ということ。
この時、以下が成り立つ。
証明1についての説明
まずは指示関数で h(x)が ηの大小に比べてと切り分ける。
そして、 h(x)≤ηの部分では上下に p(x)をかけ、 h(x)>ηの部分では上下に p(x,s=+1)をかけた。
さらに、 σ(x)=p(s=+1∣x)で書き直せる部分を書きなおすと、 p(x),p(x,s=+1)についての期待値に分割できる。前半はそのまま使えるが、後半に関しては、
p(x,s=+1)=p(x,s=+1,y=+1)+p(x,s=+1,y=−1)=p(y=+1)p(x,s=+1∣y=+1)+p(y=−1,s=+1)p(x∣y=−1,s=+1)=p(y=+1)p(x∣y=+1)+p(y=−1,s=+1)p(x∣y=−1,s=+1)=πp(x∣y=+1)+ρp(x∣y=−1,s=+1) となる。ここでは、PU Learningの前提である p(s=+1∣x,y=+1)=1を使って1項目を式変形した。
このように、既知で計算できる期待値に落とし込んでいる。
上の式のように、既知の期待値に落とし込んでいる。 η以下の h(x)を取るなら、 xのラベルが決してつかないという形。また、↑の式は実際に訓練するときすべてのPositive, Negative, Unlabeledを使うのではなく、オリジナルに考えた h,ηという関数や値で条件に満たすものだけを使うという形。
理想的には、 hも σとほぼ同じ関数であることらしい。この時、 h(x)が1に近ければ σ(x)も1にほぼ近くなり、ほぼ確実にラベルがつく、ということになる。そうすれば、上の式の第2,3項目に集計される。逆に h(x)が小さいときには第1項目に集計される感じ。
この ηは重要なハイパーパラメタである。大きいほど、Unlabeledについて重きを置くということになる。
既存の手法はrisk functionをUだけで推定していたが、重みを軽くしてもUが多すぎてNegativeに偏ってしまう、cost-sensitive特有の予測がマイナスに偏る問題(Minibatch内でPositiveがないようなMinibatchが出てくるみたいな)があった。
これについて、データをあえて一部は使わないという大胆な発想で回避するスキームが確かに考えられる。
実装するには
実用上、 σ(x)は推定された σ^(x)となり、これを h(x)とする。(これまじでいいの?) また、上手く ηを選ぶことも重要。
ηの選び方
直接推計するのが難しいので、中間変数 τを新たに置いて、以下のようだと仮定する。推計が難しいからこそ、下記条件を満たすものの個数を τを使って推定する。 (1−π−ρ)nUとなっているのは、以下の定義の部分で今推計してる部分が 1−π−ρの重みであるから。
Opinion: 二分探索とかで推定できない?
{x∈XU∣σ^(x)≤η}の個数=floor(τ(1−π−ρ)nU) 高精度の σ^があるときは、 τを大きくして(Unlabeledを多く取り込んで)計算する。そうでない σ^が正確に推定できない場合は、 τは小さくして(Unlabeledを少なく使いながら)計算する。
σ^の推計方法
PositiveとBiased NegativeをPositiveと見なして、UnlabeledをそのままとしてuuPUをすれば、疑似的に σ^(x)が得られる。
ただし、計算はこれに限る必要はなく、密度比推定(Kanamori 2009)などのようにでもOK。
なお、appendix Cにあるように、以下の式で σ^を最小化しても良い。
具体的な実装
シャッフルしてmini batchでやる。DNNでのやり方として普通のやり方。
性能の理論的評価
Appendixに詳細にある。risk functionを提案した形に分解しているが、基本は
🚫
 Post not found と同じ感じで証明できる。3つの式を合成して1つにするときは 1−δ/3以上の確率で、として式変形していた。
Post not found と同じ感じで証明できる。3つの式を合成して1つにするときは 1−δ/3以上の確率で、として式変形していた。
PU Learning Revisited
biased Negativeがなくても、この手法が提案した閾値 σ^(x)>ηの考えはPU Learningにも使える。この手法はPUbN\Nと命名されている。
Negativeがないので、 s=+1,y=+1ors=+1,y=−1の条件分けはなくなり1つにまとまる。そして、展開した中でもNegative部分が消えている。
これは実質的に、Unlabeledのデータの選別なので、ある意味Sample-Selectionであると言える。これによって、Unlabeledが実質的なNegativeとして扱われて薄くしても、Negativeにかたよりがちなのを改善できる。
実験
全部書くのは長すぎるので、大事なところだけ
使った損失関数はsigmoid loss。使ったデータセットはMNIST、CIFAR-10、20 News groups。使ったネットはConvNet、PreAct ResNet-18だそう。
比較に使ったのはnnPNUのみ。
biased Negativeのアノテーションは、 z∈{1,⋯,S}として、カテゴリをまず考える。各カテゴリについて、以下が成り立つ。
p(x∣z,y=−1)=p(x∣z,y=−1,s=+1)p(z∣y=−1)=p(z∣y=−1,s=+1) つまり、同じカテゴリに属していれば、ラベルがついてるかどうかによってデータの生成分布は全く同じ。
これ、生成として何を意味してるんだ?実験を見ると、biased Negative=指定のカテゴリにのみ属するNegativeを生成、らしい。
2017-ICML-[PNU]Semi-Supervised Classification Based on Classification from Positive and Unlabeled Data で提案されたPNU Learningという手法がある。PNU Learningのリスクは、PNとPU or NUの適宜な割合 での混合比で混ぜたものである
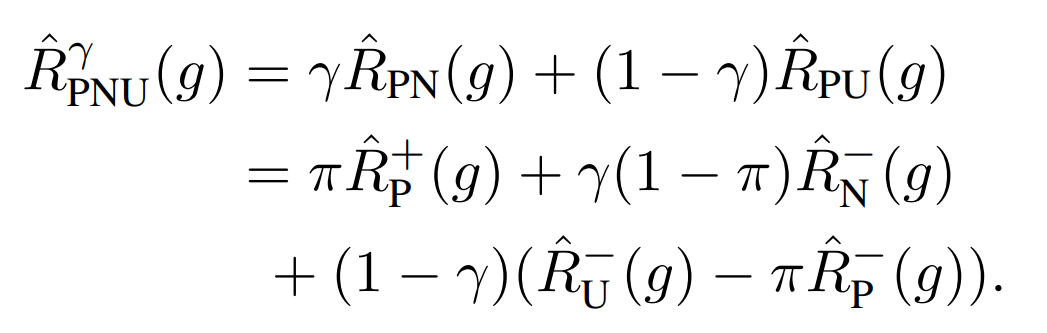
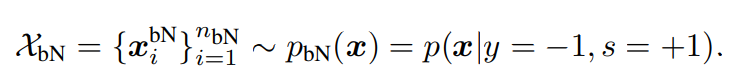
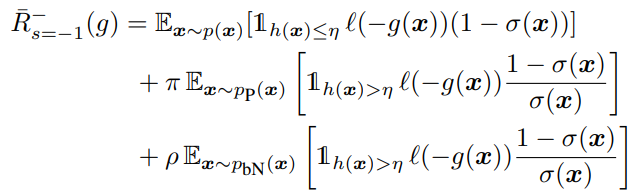
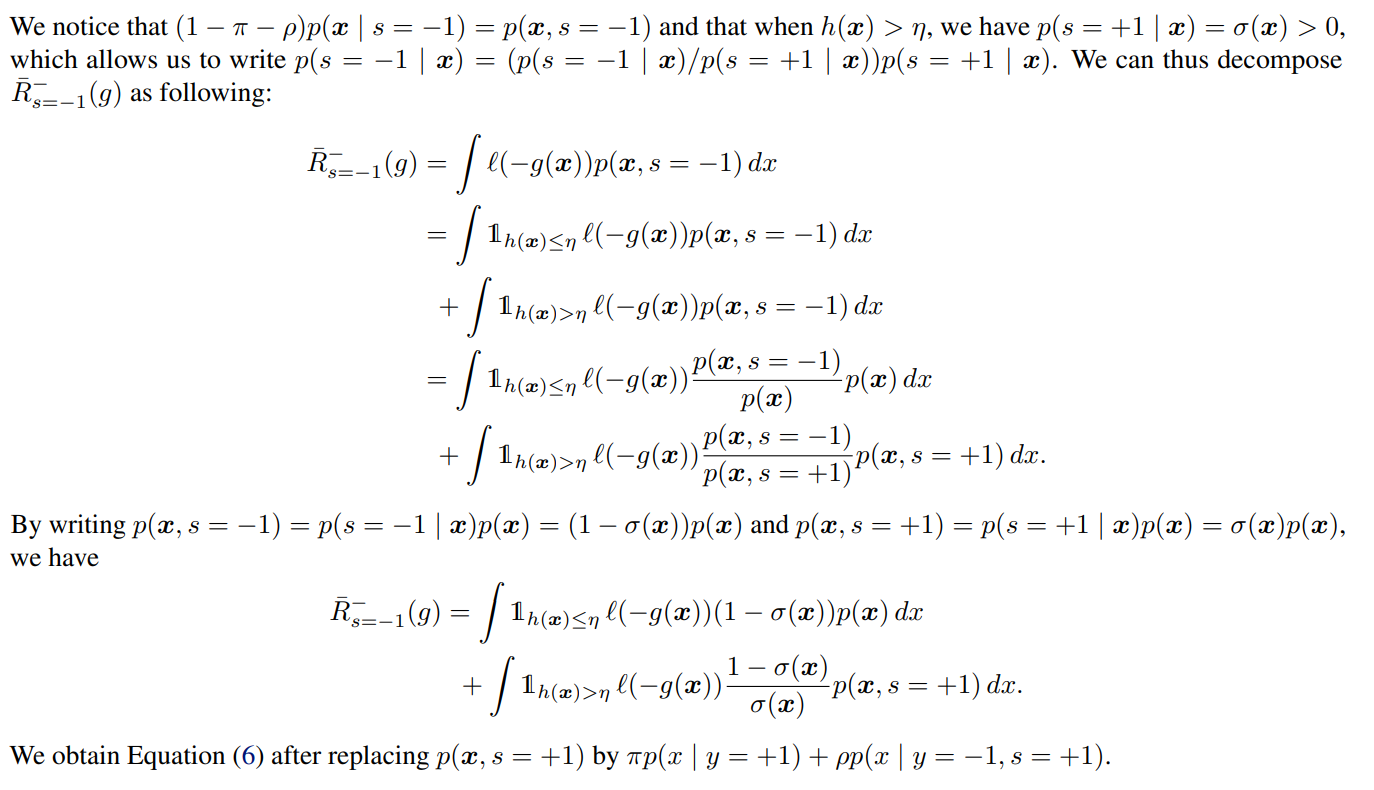
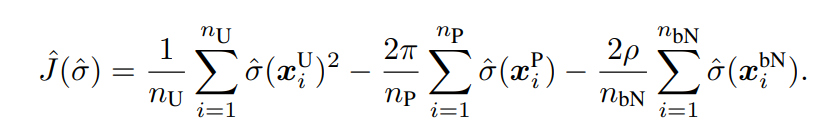

Post not found と同じ感じで証明できる。3つの式を合成して1つにするときは 以上の確率で、として式変形していた。